你真的了解R²吗？

共计 7742 个字符，预计需要花费 20 分钟才能阅读完成。

一、引言

你真的了解R²吗？

当你骄傲地展示一个R²=0.95的模型时，全场掌声雷动。

但如果这个模型在新数据上表现惨败呢？

在构建统计模型时，R²（决定系数）往往是分析师和数据科学家最先引用的指标之一。它广泛出现在学术论文、行业报告和研究中——但也是最常被误解或误用的指标之一。

高R²值真的代表模型优秀吗？仅凭R²就足以评估模型性能吗？校正R²和预测R²又有什么不同？

本文将深入探讨：

• R²、校正R²与预测R²的真实含义；
• 为什么单纯依赖R²会误导决策；
• 如何结合解释力与预测力评估模型；
• 通过R语言{tidymodels}框架的实战演示。

我们还将讨论最佳实践、常见陷阱，并帮助你建立超越表面模型摘要的评估思维。

二、理论背景

2.1 什么是R²？

决定系数R²定义为：

为残差平方和  = 

为总平方和 = 

它告诉我们模型解释的方差比例。R²为0.80意味着因变量中80%的可变性可以由模型解释。

但要注意，它只衡量训练数据的适合度，而不是模型的泛化能力。

2.2 校正R2

当我们向回归模型中添加预测因子时，R²永远不会减小——即使添加的变量是无关的。

校正R²通过惩罚预测因子的数量来纠正这一点：

n：观察数量；

p：预测数量。

因此，校正R²只有在新的预测器对模型的改进超过偶然预期的情况下才会增加。

2.3 预测R2

预测R²（或交叉验证R²）是对模型效用最诚实的估计。它回答了这个问题:

这个模型能在多大程度上预测新的、看不见的数据？

这通常是使用交叉验证计算的，与常规的R²不同，它反映了样本外性能。

你也可以把它看作：

其中PRESS为基于交叉验证的预测误差平方和。

三、数据集的概述

我们将使用经典的波士顿住房（Boston Housing）数据集来演示。它包括:

波士顿506个郊区的社会经济和住房变量

目标：medv（自住房屋价值中位数，以1000美元为单位）

以下是关键变量：

• crim：各城镇的人均犯罪率；
• zn：为大型用地的居住用地比例；
• indus：占非零售业务面积的比例；
• chas：查尔斯河虚拟变量(1 =河道边界河；0 =否则)；
• nox：一氧化氮浓度（千万分之一）；
• rm：每套住宅的平均房间数；
• age：1940年以前建造的自住单位的比例；
• dis：与就业中心的加权距离；
• rad：径向公路可达性指数；
• tax：每1万美元征收房产税；
• ptratio：按城镇划分的师生比例；
• black：1000(Bk – 0.63)^2，其中Bk是黑人居民的比例
• lstat：社会地位较低的人口比例
• medv：目标-自住房屋的中位数价值（单位：1000美元）

这个回归问题模仿了常见的房地产或社会经济建模用例。让我们首先检查数据集的汇总统计信息。

library(tidymodels)
library(MASS)
library(ggplot2)
library(corrr)
library(skimr)
library(patchwork)


boston <-MASS::Boston
skim(boston)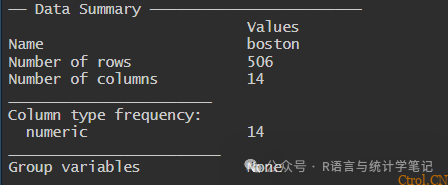

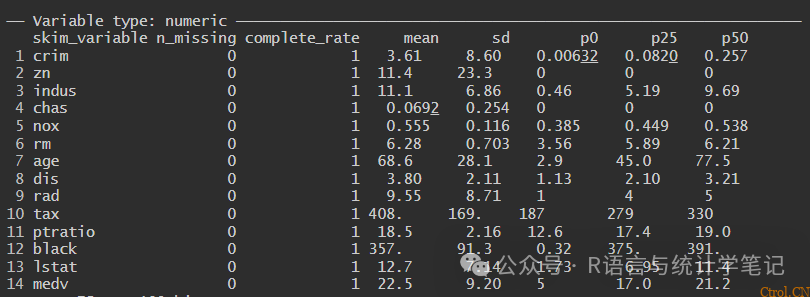
接下来，我们检查与medv的相关性：

boston %>%correlate()%>% corrr::focus(medv)%>%arrange(desc(medv))

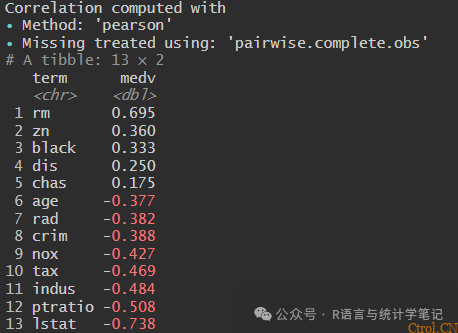
相关性的解释：

• rm与medv呈显著正相关——房间越多，价值越高。
• lstat和crim呈显著负相关——地位越低或犯罪率越高，房价就越低。
• nox、age和ptratio也与medv呈负相关，暗示了社会环境影响。

这些见解将指导我们构建和评估我们的模型。

四、探索性数据分析

让我们可视化一些与目标变量medv相关的最具影响力的变量。这些探索性图形有助于揭示潜在的线性或非线性关系、异常值或转换需求。

# Define individual plots with improved formatting forQuarto rendering
p1 <-ggplot(boston,aes(rm, medv))+
geom_point(alpha =0.5, color ="#2c7fb8")+
geom_smooth(method ="lm", se =FALSE, color ="black")+
labs(
    title ="Rooms\nvs. Median Value",
    x ="Average Number of Rooms (rm)",
    y ="Median Value of Homes ($1000s)"
)+
theme_minimal()+
theme(plot.title=element_text(size =11, lineheight =1.1))

p2 <-ggplot(boston,aes(lstat, medv))+
geom_point(alpha =0.5, color ="#de2d26")+
geom_smooth(method ="loess", se =FALSE, color ="black")+
labs(
    title ="Lower Status %\nvs. Median Value",
    x ="% Lower Status Population (lstat)",
    y ="Median Value of Homes ($1000s)"
)+
theme_minimal()+
theme(plot.title=element_text(size =11, lineheight =1.1))

p3 <-ggplot(boston,aes(nox, medv))+
geom_point(alpha =0.5, color ="#31a354")+
geom_smooth(method ="loess", se =FALSE, color ="black")+
labs(
    title ="NOx Concentration\nvs. Median Value",
    x ="NOx concentration (ppm)",
    y ="Median Value of Homes ($1000s)"
)+
theme_minimal()+
theme(plot.title=element_text(size =11, lineheight =1.1))

p4 <-ggplot(boston,aes(age, medv))+
geom_point(alpha =0.5, color ="#ff7f00")+
geom_smooth(method ="loess", se =FALSE, color ="black")+
labs(
    title ="Old Homes %\nvs. Median Value",
    x ="% Homes Built Before 1940 (age)",
    y ="Median Value of Homes ($1000s)"
)+
theme_minimal()+
theme(plot.title=element_text(size =11, lineheight =1.1))

p5 <-ggplot(boston,aes(tax, medv))+
geom_point(alpha =0.5, color ="#6a3d9a")+
geom_smooth(method ="loess", se =FALSE, color ="black")+
labs(
    title ="Tax Rate\nvs. Median Value",
    x ="Tax Rate (per $10,000)",
    y ="Median Value of Homes ($1000s)"
)+
theme_minimal()+
theme(plot.title=element_text(size =11, lineheight =1.1))

p6 <-ggplot(boston,aes(dis, medv))+
geom_point(alpha =0.5, color ="#1f78b4")+
geom_smooth(method ="loess", se =FALSE, color ="black")+
labs(
    title ="Distance to Jobs\nvs. Median Value",
    x ="Weighted Distance to Employment Centers (dis)",
    y ="Median Value of Homes ($1000s)"
)+
theme_minimal()+
theme(plot.title=element_text(size =11, lineheight =1.1))

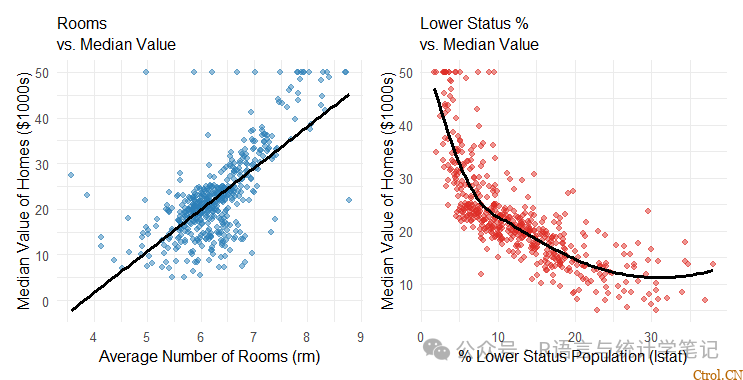
(p1 | p2)+plot_layout(guides ='collect')

• 房间（rm）：与medv有很强的正线性关系。房间越多，房屋价值越高。
• 低地位人口（lstat）：强非线性反比关系。贫困地区的房价往往要低得多。

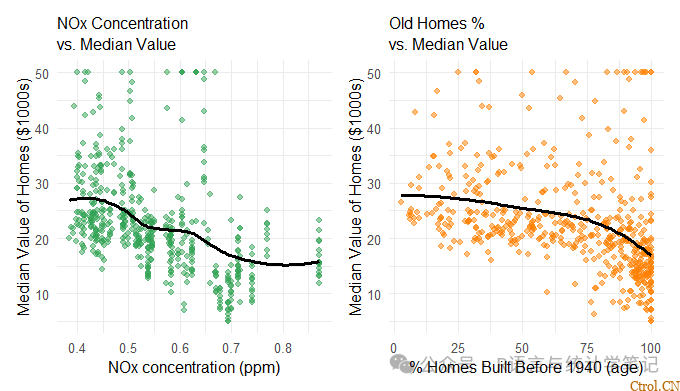
(p3 | p4)+plot_layout(guides ='collect')

• 一氧化氮（nox）：中度负相关-污染等环境因素影响价格。
• 老房子（age）：轻微的负面趋势——老房子的吸引力或价值可能会降低。

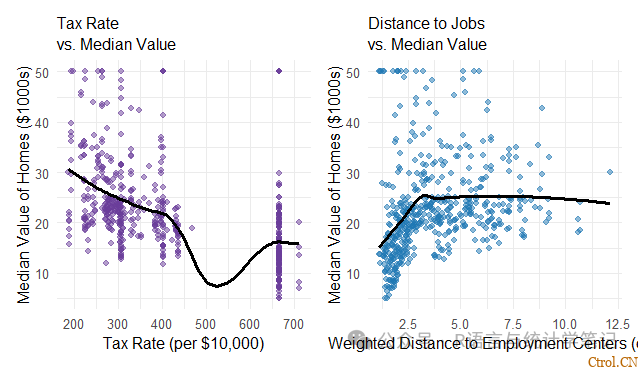
(p5 | p6)+plot_layout(guides ='collect')

• 税率（tax）：较高的税率往往与较低的房屋价值有关，可能是由于地理位置或社会经济的限制。
• 到就业中心的距离（dis）：弱至中度正相关。郊区或交通发达的地区可能需要更高的价值。

这六个图结合了住房价值的社会经济和环境维度——提供了直觉和建模方向。

五、使用Tidymodels建模

现在我们已经研究了数据，现在是使用tidymodels框架拟合模型的时候了。我们将使用简单的线性回归来预测medv，即房屋价值中位数。

5.1数据分割与预处理

我们首先将数据集分成训练集和测试集。训练集将用于拟合模型，测试集将评估其泛化性能。

set.seed(42)
split <-initial_split(boston, prop =0.8)
train <-training(split)
test <-testing(split)

rec <-recipe(medv ~., data = train)
model <-linear_reg()%>%set_engine("lm")
workflow <-workflow()%>%add_recipe(rec)%>%add_model(model)

5.2模型拟合

现在我们将模型拟合到训练数据中：

fit <-fit(workflow, data = train)

5.3在训练集上评估模型

我们从拟合模型中提取R²和Adjusted R²值：

training_summary <-glance(extract_fit_parsnip(fit))
training_summary %>% dplyr::select(r.squared, adj.r.squared)

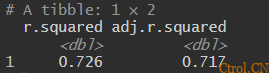
解释:

• R²衡量由训练集中的预测变量解释的medv中方差的比例。
• 校正R²通过惩罚预测因子的数量来调整该值，使其在多变量环境中更可靠。
• 如果R²和校正R²差异显著，则表明某些预测因子可能对模型没有意义。

例如：一个有12个预测因子的模型可能显示R²= 0.76，但校正R²= 0.72——这表明一些预测因子增加了复杂性，但没有真正的解释力。

5.4测试集性能

现在我们在未见过的测试数据上评估模型：

preds <-predict(fit, test)%>%bind_cols(test)
metrics(preds, truth = medv, estimate =.pred)

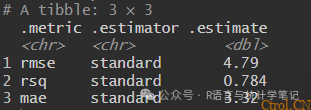
解释:

• 如果测试R²远低于训练R²，则可能存在过拟合。
• 如果测试RMSE很高，则模型的绝对预测误差很大——这是泛化不良的另一个标志。

5.5预测R2的交叉验证

为了获得更稳健的性能估计，我们使用了10倍交叉验证：

set.seed(42)
cv <-vfold_cv(train, v =10)
resample <-fit_resamples(
  workflow,
  resamples = cv,
  metrics =metric_set(rsq, rmse),
  control =control_resamples(save_pred =TRUE)
)
collect_metrics(resample)

解释:

• 预测的R²（通过CV）告诉我们模型在多个样本中对未知数据的表现如何。
• 它通常位于训练R²和测试R²之间。
• 交叉验证和检验R²之间的一致性表明模型是稳定的。

提示

• 使用交叉验证作为标准评估工具，特别是在数据有限的情况下。
• 调查结果摘要：
• 我们的线性模型解释了很大一部分方差，但一些预测因子可能是无关的或冗余的。
• 交叉验证确认模型是相对稳定的，但留下了改进的空间——可能是通过特征选择或非线性建模。

下一步，我们可以分析残差或探索模型改进，如多项式项或正则化。

5.6残差诊断

现在让我们检查一下我们的线性模型是否满足基本的回归假设。我们将绘制残差并评估模式、非线性和潜在的异方差。

library(broom)
library(ggthemes)

aug <-augment(fit$fit$fit$fit)

ggplot(aug,aes(.fitted,.resid))+
geom_point(alpha =0.5, color ="#2c7fb8")+
geom_hline(yintercept =0, linetype ="dashed")+
labs(
    title ="Residuals vs Fitted Values",
    x ="Fitted Values",
    y ="Residuals"
)+
theme_minimal()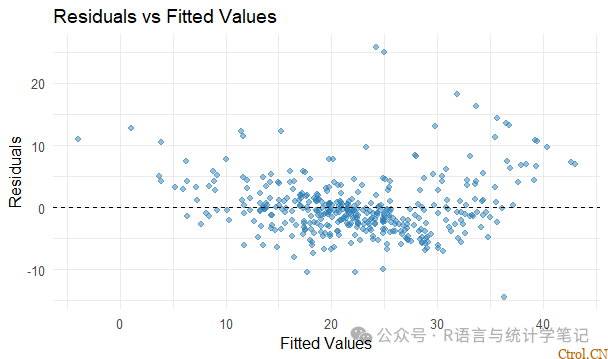

解释：

• 我们希望残差随机分布在0附近。
• 如果有一个模式或漏斗形状，这可能表明非线性或异方差

5.7改进模型：转换lstat

从前面的EDA中，我们看到lstat（较低的状态%）和medv之间存在强烈的非线性关系。我们试试log-transforminglstat来获取曲率。

5.7.1转化后的更新配方

rec_log <-recipe(medv ~., data = train)%>%
step_log(lstat)

workflow_log <-workflow()%>%
add_model(model)%>%
add_recipe(rec_log)

fit_log <-fit(workflow_log, data = train)

5.7.2转换模型的评价

preds_log <-predict(fit_log, test)%>%bind_cols(test)
metrics(preds_log, truth = medv, estimate =.pred)

# Atibble:3 × 3
.metric.estimator.estimate
<chr><chr><dbl>
1 rmse    standard       4.43 
2 rsq     standard       0.815
3 mae     standard       3.16 

glance(fit_log)
# Atibble:1 × 12
  r.squared adj.r.squared sigma statistic   p.value    df logLik   AICBIC deviance
<dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl>
1     0.785         0.778  4.21      110. 2.64e-121    13 -1147. 2324. 2384.    6911.
# ℹ 2 more variables: df.residual <int>, nobs <int>

解释：

• 比较转换后的模型与原始模型的RMSE和R²。
• 如果我们看到改进，则转换有助于捕获潜在的非线性。
• 校正R²在评估转换是否真正改善了拟合（而不仅仅是过拟合）时特别有用。

提示

• 变换、多项式项和样条都是在不放弃可解释性的情况下改进线性模型的有效策略。
• 检查残差并测试转换后，我们的下一步可能是探索正则化模型，如ridge或lasso回归，甚至超越线性，使用基于树的模型。

六、常见误区与迷思

尽管R²被广泛使用且直观易懂，但即便是经验丰富的分析师也常误解其含义。本文超越教科书定义，揭示关于R²及其变体的现实陷阱与认知偏差。

迷思1：高R²等于好模型

R²=0.95看似惊艳，但未必具有预测力：

• R²可能源于过拟合（尤其当模型复杂或变量过多时）；

• 必须结合校正R²和预测R²评估真实价值；

迷思2：增加变量总能提升模型

• R²随变量增加永不下降，但校正R²会（且应该）在新增变量无价值时降低；

• 无关变量会徒增复杂度却不增强解释力；

• 这属于维度过拟合的典型表现；

迷思3：R²暗示因果关系

• R²衡量相关性而非因果性；

• 高R²可能来自伪相关或混杂变量；

• 必须辅以领域知识和因果推理；

迷思4：R²是通用评估指标

• R²仅适用于回归任务，用于分类模型毫无意义；

• 二分类问题应使用AUC、准确率、精确率、召回率等指标；

迷思5：R²高就不需检查残差图

• 高R²不保证满足模型假设；

• 残差模式仍可能揭示非线性、异方差性或强影响力异常点；

• 务必进行残差诊断；

迷思6：预测R²无关紧要

• 多数人只报告R²和校正R²，却忽略交叉验证；

• 预测R²（如通过10折交叉验证）才是模型泛化能力的诚实指标；

迷思7：R²有固定解释标准

• R²值需结合领域背景：社会科学中0.3可能很有意义，而物理学要求0.99+；

• “低”R²未必无用——可能反映人类行为或宏观经济数据的固有波动性；

核心洞见

永远在完整语境中使用R²——结合其他指标、验证策略和图形检验。

七、结论与建议

7.1 核心总结

本文深度解析了R²、校正R²和预测R²——不仅是数学概念，更是建模批判性思维的工具。我们探讨了理论框架、tidymodels实践应用、残差诊断以及通过变量转化提升模型的方法。

关键结论：

R²反映训练数据拟合度，但单独使用具有误导性

校正R²通过惩罚模型复杂度改进R²

基于交叉验证的预测R²才是最可靠的真实表现评估

高R²值极具诱惑力，但正如我们所见，它无法保证因果性、泛化性或正确性。唯有将R²与残差诊断、领域知识和样本外验证结合，才能做出负责任模型评估。

7.2 实践建议

• 永远同时报告R²、校正R²和预测R²——拒绝单一指标依赖；

• 执行残差诊断检验线性假设、方差稳定性和异常点影响；

• 默认采用交叉验证（如10折）策略，尤其在小数据集场景；

• 对非线性变量进行转换（如处理lstat变量）或使用灵活模型（样条/GAM等）；

• 避免纳入无关变量——它们会虚增R²却不提升泛化能力；

• 结合领域背景解读R²——某些领域低R²仍有价值，另一些领域则可能预示模型缺陷；

• 用可视化工具（散点图、预测-实际值图、残差图）补充数值指标；

7.3 进阶方向

若想进一步提升建模能力：

• 尝试岭回归/lasso回归处理多重共线性；

• 当关系复杂非线性时，探索树模型（如随机森林）；

• 使用yardstick/modeltime等工具自动化验证与报告；

最终启示

建模的真谛不在于最大化R²，而在于理解数据、验证决策并做出可靠预测。

（全文完）