共计 2439 个字符，预计需要花费 7 分钟才能阅读完成。
1. 阻尼的含义与分类
在结构动力学分析中，阻尼对模态分析结果的影响较小，可以不考虑。但对于谐响应分析，响应谱分析，随机振动分析，以及瞬态分析，阻尼大小对分析结果的影响明显，不可忽略。阻尼是能量耗散的一种表现，它来源于结构连接处的摩擦和局部材料的迟滞效应。
1.1 阻尼的分类
与速度成正比的阻尼称之为粘性阻尼（viscous damping）。有时粘性阻尼不能满足工程需求，因此，还有与摩擦力相关的库伦阻尼，结构阻尼，流体阻尼等。
粘性阻尼是与速度成正比的阻尼类型，其数学表达式如下：
在这个公式中：
代表由粘性阻尼产生的力（通常以牛顿为单位）。
是阻尼系数，它是一个正实数，表示每单位速度所产生的阻尼力的大小（通常以牛顿·秒/米为单位）。
是速度，即位移对时间的导数（通常以米/秒为单位）。
这个公式说明了阻尼力是如何与结构的速度成正比的，即结构移动得越快，受到的阻尼力就越大，从而导致能量的耗散。阻尼的存在使得结构在受到动态荷载后，能够在较短的时间内恢复到静止状态，而不是无限期地振荡。尽管粘性阻尼的物理意义相对清晰，但阻尼更深层次的机理仍在不断研究和发展中。
2. 阻尼对结构动态响应的影响
阻尼的大小会影响系统的动态响应。阻尼比ξ定义了有阻尼固有频率ωd与无阻尼固有频率ω之间的关系：
。
当然，关于阻尼比的公式可以整理如下：
- ξ代表阻尼比，它是一个无量纲的比例系数，用于描述阻尼的相对大小。
是该模态的阻尼系数，表示每单位速度所产生的阻尼力的大小。
是该模态的临界阻尼系数，它是实现临界阻尼状态所需的阻尼系数，即结构在受到扰动后能在一个周期内恢复到平衡状态的最大阻尼。
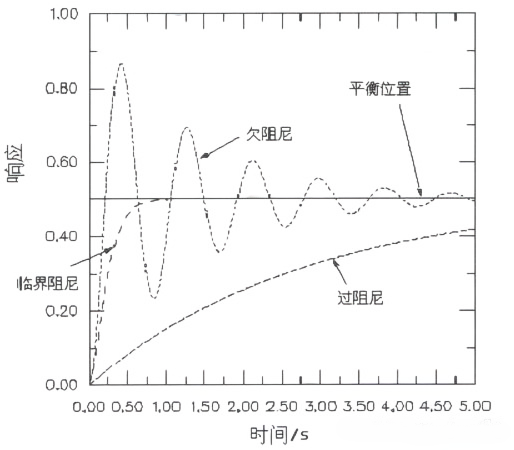
当结构处于临界阻尼时，施加一个扰动后，结构不会振荡，而是尽可能迅速的恢复到它的初始静止构型，如下图所示。
不同阻尼比ξ条件下的位移时程曲线的特征：
无阻尼振动（阻尼比ξ=0），振幅不衰减。
欠阻尼振动（阻尼比0<ξ<1），振幅逐渐衰减，也就是恢复到平衡状态的时间超过一个周期。
临界阻尼振动（阻尼比ξ=1），振动到一个周期，振幅刚好衰减到0，也就是恢复到平衡状态的时间刚好为一个周期。
过阻尼振动（阻尼比ξ>1），因为过阻尼的时候阻尼力比临界阻尼时候大，趋于平衡状态的时候总的恢复力小，自然表现出来的就是衰减比临界阻尼的要慢。
3. Abaqus中的阻尼设置方式
Abaqus的阻尼分为与速度成比例的粘性阻尼和与位移成比例的结构阻尼。
abaqus阻尼设置可分为三种方式：
- 材料和单元的阻尼
- 整体阻尼，包括粘性阻尼，瑞利阻尼，结构阻尼
- 模态阻尼，只能用于模态分析
在ABAQUS中阻尼可以应用在下面的动力学分析中：
- 非线性问题直接积分求解（显式分析或者隐式分析）
- 直接法或子空间法稳态动力学分析
- 模态动力学分析（线性）
3.1 ANSA-Abaqus中阻尼设置
针对模态动力学分析，在ABAQUS/Standard中可定义几种不同类型的阻尼：直接模态阻尼（DirectModal Damping），瑞利阻尼（RayleighDamping），复合模态阻尼（Composite Modal Damping）和结构阻尼（StructureDamping），粘性阻尼（VISCOUS）。
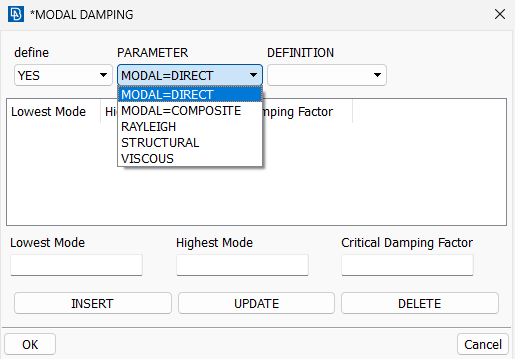
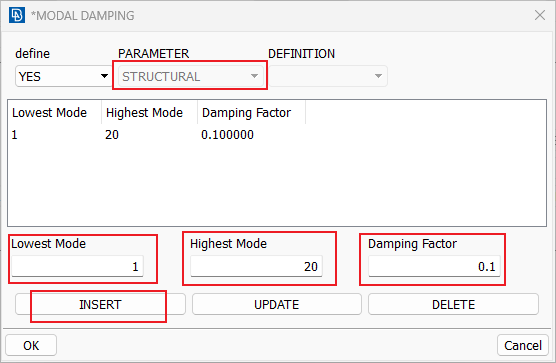
3.1.1 直接模态阻尼（DirectModal Damping）
直接模态阻尼允许用户精确定义系统的每阶模态的阻尼，典型取值范围在临界阻尼比ξ为1%~10%之间。通常取值为0.02或者0.05较多。
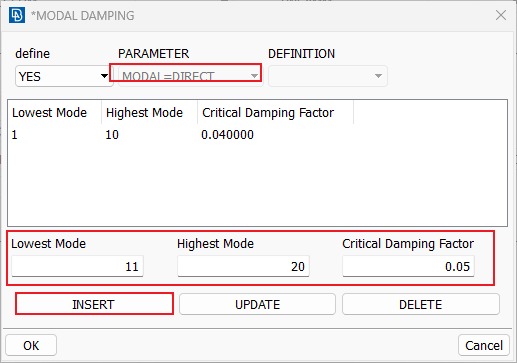
举例：设置前10阶振型的阻尼定义为4%的临界模态阻尼，11~20阶振型的阻尼为5%的临界阻尼
在MODAL DAMPING界面中，分别在Lowest MODE和Highest Mode分别输入模态阶次，在Critical Damping Factor中输入阻尼比ξ，然后点击INSEERT。
3.1.2 瑞利阻尼（RayleighDamping）
在瑞利阻尼中，假设阻尼矩阵可表示为质量矩阵和刚度矩阵的线性组合，即：
[C]=α[M]+β[K][?]=?[?]+?[?]（C为阻尼，M为质量，K为刚度）
ABAQUS中通过设置alpha和beta来求解瑞利阻尼，具体如下图。?与质量矩阵有关，?与刚度矩阵有关，而alpha与beta与阻尼比的关系如下：
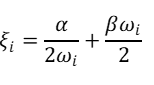
假设阻尼比为0.05，频率范围为0.1Hz-20Hz，推导质量系数和刚度系数。
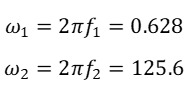
求解下面二元一次方程组，得alpha=0.0625，beta=0.0008。
在MODAL DAMPING界面中，选择RAYLEIGH后，分别在Lowest MODE和Highest Mode分别输入模态阶次，在Mass damping中输入?的值0.0625，在Stiffness Damping中输入?的值0.0008，然后点击INSEERT。
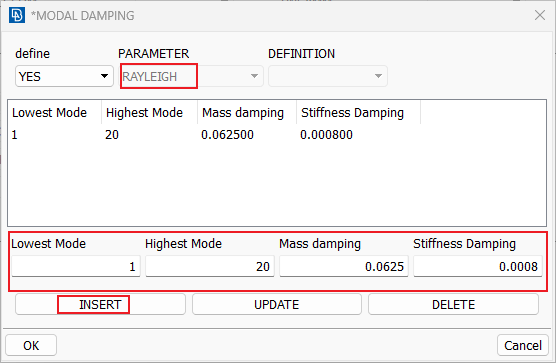
注意：瑞利阻尼模型对于大阻尼系统（阻尼值超过10%临界阻尼）是不可靠的。
3.1.3 复合模态阻尼（Composite Modal Damping）
在复合阻尼中，对应于每种材料的阻尼定义一个临界阻尼比，这样就得到了对应于整体结构的复合阻尼。如果结构由多种材料组成，那么采用复合阻尼来描述系统的阻尼特性是非常简便有效的。
在ANSA-ABAQUS中分两步定义复合阻尼。
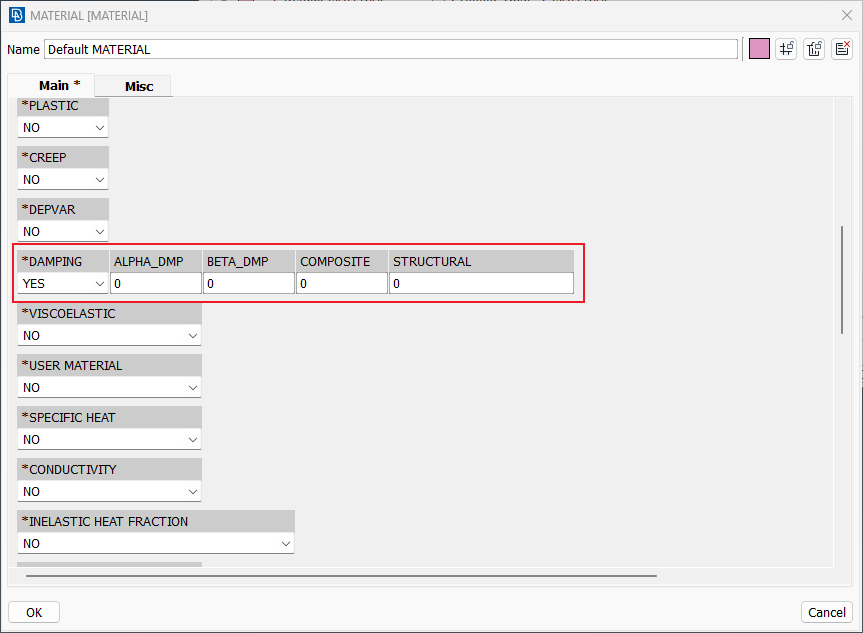
a) 在材料属性中定义该材料对应的复合阻尼，如下图所示：
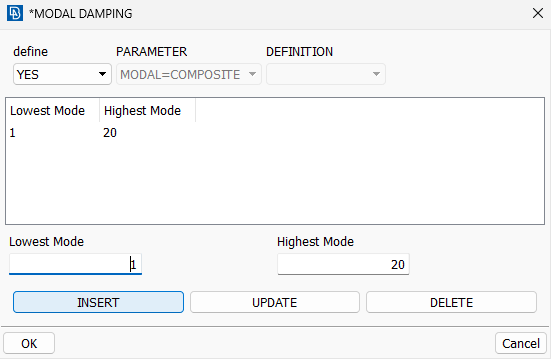
b) 在分析步骤内勾选复合阻尼选项，如下图所示：
3.1.4 结构阻尼（StructureDamping）
系统的结构阻尼特性与结构或者材料的内摩擦机理有关。结构阻尼力的方向与速度方向相反，与位移相比滞后90°。只有当位移和速度的相位差为90°时，结构阻尼假设才能成立，因此激励必须是正弦函数。使用结构阻尼假设的动力学分析包括稳态响应分析和随机响应分析，其它如瞬态动力学分析则不能直接应用机构阻尼，必须依据一定的准则将其转换为等效的粘性阻尼。
abaqus中的structural Damping一般就是指的材料的损耗因子。结构阻尼系数约为阻尼比ξ的2倍。
详细计算过程可参考《结构阻尼与材料阻尼的关系》。
假设阻尼比ξ为0.05，则结构阻尼系数设置为0.1。
